کمی سلبریتیبازی!
فرهنگ سلبریتی این روزها داغ است. هر کدام از ما، سلبریتیهای محبوب خود را داریم؛ از بازیگر گرفته تا فوتبالیست و مدل و خواننده یا دانشمند!
همه دوست داریم سلبریتی محبوبمان را ببینیم، با او گفتوگو کنیم و سِلفی بگیریم. بخش قابل توجهی از محتوای رسانههای اجتماعی مجازی نیز به سلبریتیها اختصاص دارد.
شما تا به حال سلبریتی محبوب خودتان را دیدهاید؟
به نظرتان چقدر احتمال دارد که سلبریتی عزیزتان را به طور اتفاقی در خیابان ببینید؟
اگر زمانی کسی را در خیابان ببینید که کاملاً شبیه به سلبریتی مورد علاقهٔ شماست، چقدر احتمال دارد که واقعاً خودش باشد؟
سکانس نخست: امروز سلبریتی محبوبم را دیدم!
از شما میخواهم تلاش کنید و از قوهٔ تخیّل خودتان استفاده کنید.
فرض کنید در یکی از شهرهای نسبتاً کوچک ایران زندگی میکنید و در یکی از محلههای آن ساکن هستید که نه بالاشهر محسوب میشود و نه پایینشهر. یکی از روزهایی که برای قدم زدن و خرید بیرون رفتهاید، در ازدحام جمعیت یکی از سلبریتیهای مشهور و مورد علاقهٔ خود را میبینید.
از فرط تعجب خشکتان میزند و زبانتان بند میآید. با خود فکر میکنید:
نههه! من و این همه خوشبختی!؟ محاااله.
تا از شوک به در آیید و همچون آنها که تا به حال انسان ندیدهاند برای سلفی و امضا و اظهار شیفتگی به سمت سلبریتی محبوبتان هجوم ببرید، در میان جمعیت محو شده و تنها گرد و خاک رفتنش نصیبتان میشود. او به سرعت از شما دور شده است.
به خانه میرسید؛ لباسهایتان را درنیاورده، تمام خانواده را جمع میکنید تا داستان این مواجهه را برایشان بازگو کنید.
پس از بازگو کردن داستانِ خود، با هیجان بسیار به صورت اعضای خانواده نگاهی میاندازید تا شور و شوقی را در چشمانشان ببینید. اما با کمال تعجب متوجه میشوید که همه با نگاهی عاقل اندر سَفیه، ابرو بالا انداختهاند و به نشانهٔ تأسف سر تکان میدهند.
برادرتان با لحن تمسخر میگوید:
آخه بــــیعقل! یه خرده فکر کن پیش خودت! ببین چقدر احتمال داره آدمی مثل اون پا شه بیاد توی محلهٔ ما؟! مگه خُله؟ چی کار باید داشته باشه که بیاد اینجا؟ اومده سر کوچهٔ ما ماست بخره؟! به خدا عقل نداری راحتیا!
پدر و مادرتان با اینکه نمیدانند دربارهٔ چه کسی صحبت میکنید، در ابراز تأسف برایتان چیزی کم نمیگذارند!
از نظر اعضای خانوادهٔ شما، چنین چیزی اصلاً ممکن نیست یا احتمالش بسیار کم است. شما نیز با شنیدن نظر خانواده، به خود شک میکنید:
راست میگن! واقعاً چند درصد احتمال داره که اونی که دیدم سلبریتی عزیزم باشه، نه یه آدم عادی که فقط بهش شبیهه؟ خب، راست میگن؛ محلهٔ ما «باکلاس» نیست و از جایی که اون زندگی میکنه، خیلی دوره! چرا بیاد اینجا؟!
در نهایت به این نتیجه میرسید که واقعاً با دانشی که از محلهٔ خود دارید، احتمال دیدن سلبریتی مورد علاقهتان واقعاً کم است.

این مسئله خیلی مهم است؛ پس به هر آنچه که از دانش ریاضیتان به یاد دارید تکیه میکنید تا بفهمید چقدر احتمال دارد واقعاً سلبریتی عزیزتان را دیده باشید!
فرض کنید چنین احتمالی را نیم درصد تخمین میزنید (٪ ۰/۵) و روی دفترچهٔ یادداشت خود چنین مینویسید:
P(تجربهای که از محلهمان دارم | دیدن سلبریتی مورد علاقهام) = ۰/۵ %
ترجمهٔ این عبارت که به زبان ریاضی نوشته شده است یعنی: احتمالِ دیدن سلبریتی مورد علاقهام با توجه به دانشی که تا کنون از محلهمان دارم، عبارت است از نیم درصد.
نماد P مخفف probability یا همان احتمال است و P(A) یعنی احتمال اینکه واقعهٔ A رخ دهد.
آن خط عمودی کوچک هم یعنی «با توجه به».
سکانس دوم: احتمالِ دیدنِ سلبریتی عزیزتان بالا میرود!
اما داستان همین جا تمام نمیشود.
شما سلبریتی محبوبتان را در شبکههای اجتماعی دنبال میکنید و هر روز، بلکه هر چند ساعت یکبار، اینستاگرام خود را برای دیدن وی و پستهایش چک میکنید!
روز بعد به یکی از پست های جدید او برمیخورید و عکسی را میبینید که وی در اینستاگرام خود منتشر کرده است. این عکس روبروی فروشگاهی زنجیرهای گرفته شده است که در محلهٔ شما یک شعبه دارد.

حال شما تقریباً مطمئن میشوید که «توهّم نزدهاید» و واقعاً سلبریتی محبوبتان را دیدهاید!
از اتاقتان بیرون میروید؛ به سمت اعضای خانواده میدوید و با هیجان فریاد میزنید که:
دیدین گفتممم؟! دیدین خُل نشدممم؟ دیدین خواب و خیال نبووود؟ واااقعاً خودش بود!
عکس او را جلوی فروشگاه زنجیرهای محلهتان به همه نشان میدهید و این بار این شما هستید که طوری آنها را نگاه میکنید که انگار با عدهای احمق سروکار دارید. :))
اما یک لحظه صبر کنید.
کاری که شما انجام دادهاید چیست؟
شما دربارهٔ احتمال دیدن سلبریتی محبوبتان تجدید نظر کردهاید.
چرا؟
چون اطلاعات جدید به دست آوردهاید. حال با در نظر گرفتن این اطلاعات جدید، برآوردتان از احتمال قبلی را از ۰/۵ درصد به ۸۵ درصد افزایش میدهید.
باز هم احتمال جدید را در دفترچهٔ یادداشت خودتان یادداشت میکنید:
P(A | B | C) = 85%
A: دیدن سلبریتی مورد علاقهام
B: تجربهای که از محلهمان دارم
C: دیدن عکس سلبریتیام در جلوی فروشگاه
اگر بخواهیم این فرمول ریاضیاتی را بخوانیم، باید بگوییم
احتمال اینکه سلبریتی محبوبم را دیده باشم با توجه به دانشی که از قبل از محلهمان دارم و با توجه به عکسی که از سلبریتی محبوبم در شبکههای اجتماعی دیدم، ۸۵ درصد است.
سکانس سوم: ناامیدی بازمیگردد!
داستان هنوز تمام نشده است.
۸۵ درصد شانس هم برای راضی شدنتان کافی نیست! برایتان مهم است قطعاً بدانید آیا واقعاً سلبریتی محبوبتان را دیدهاید یا نه. بنابراین، موقعیت شعبههای همان فروشگاهی که در محلهٔ شما هم هست و سلبریتی شما روبروی آن عکس انداخته است را در اینترنت جستوجو میکنید.
در این جستوجو، بیش از ۲۰۰ شعبهٔ دیگر از این فروشگاه زنجیرهای را در کشور پیدا میکنید. از ناراحتی آهی میکشید و بدون اینکه صدایش را دربیاورید، باز هم سراغ دفترچهٔ یادداشتتان میروید. دوباره امیدتان به این که سلبریتی محبوبتان را دیده باشید کمتر شده است. با وجود این همه شعبه، از کجا معلوم که این فروشگاه همان فروشگاه محلهٔ شما باشد؟
با در نظر گرفتن اطلاعات جدیدی که به دست آوردهاید، احتمال دیدن سلبریتی عزیزتان را از ۸۵ درصد به ۰/۳ درصد تغییر میدهید.
احتمال جدید را میتوان به زبان ریاضیاتی چنین نوشت:
P(A | B | C | D) = 0.3%
A: دیدن سلبریتی مورد علاقهام
B: تجربهای که از محلهمان دارم
C: دیدن عکس سلبریتیام در جلوی فروشگاه
D: پیدا کردن ۲۰۰ فروشگاه دیگر از همان فروشگاهی که در محله ما وجود دارد
خب، به شما تبریک میگویم. شما مفهوم آمار بِیز (Bayesian statistics) را یاد گرفتید!
حدس میزنم قبلاً چنین روشی را در محاسبهٔ احتمال پدیدهای خاص به کار نبردهاید. در آمار بیز، احتمال رخ دادن پدیدهای را با در نظر گرفتن دانش جدیدی که به دست میآوریم دائماُ بهروز میکنیم.
حال بگذارید همین سناریو را با شکل بیان کنیم:
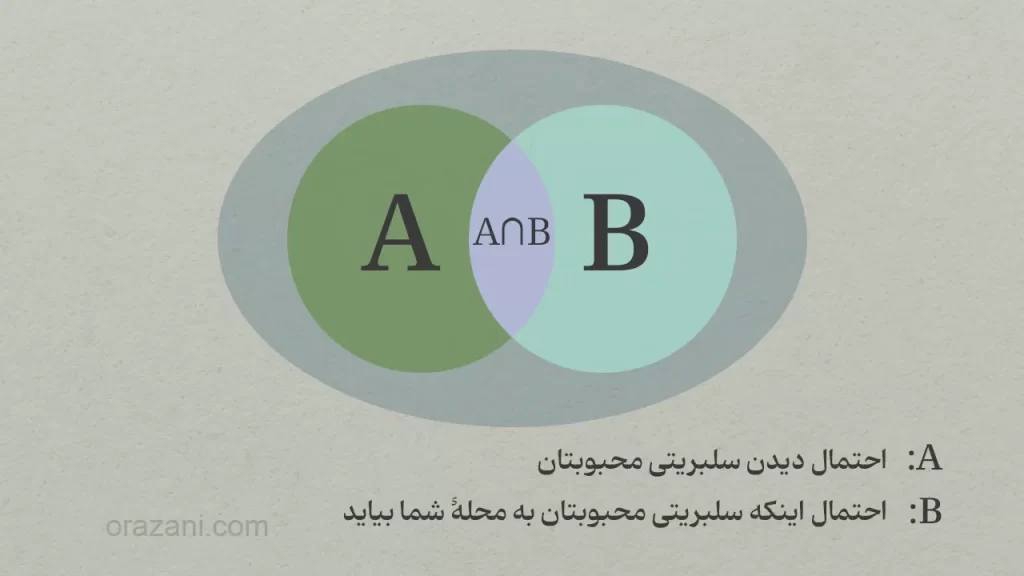
اجزای این نمودار از این قرار هستند:
- دایره A عبارت است از: احتمالِ دیدنِ سلبریتی محبوبتان
- دایره B عبارت است از: احتمال اینکه سلبریتی محبوبتان به محلهٔ شما بیاید (دانشی که دربارهٔ محلهٔ خود دارید)
- آن قسمت مشترک بین A و B نیز عبارت است از احتمال اینکه A (دیدن کسی شبیه به سلبریتی محبوبتان) و B (حضور سلبریتی در محلهٔ شما) همزمان رخ دهند.
با توجه به توضیحی که دادم، این احتمال یک احتمال شرطی (Conditional Probability) است.
چرا؟ چون به شرط اطلاعاتی که کسب میکنید، احتمال دیدن سلبریتی خود را محاسبه میکنید.
بیایید این احتمال را به زبان ریاضی بنویسیم. البته از ابتدا بگویم که از دیدن فرمولها نترسید؛ گامبهگام پیش خواهیم رفت.
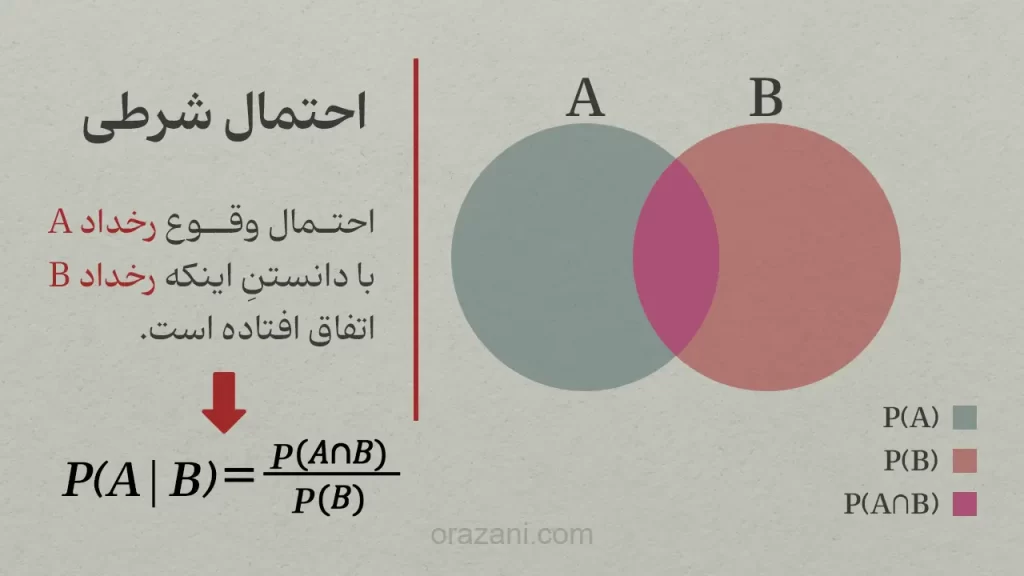
سمت چپ تساوی را میخوانیم: احتمال A به شرط B. در مثالی که آوردهام، احتمال A به شرط B یعنی احتمال اینکه سلبریتی عزیزم را دیده باشم، به شرط آن که او به محلهٔ ما آمده باشد.
اما سمت راست تساوی یعنی چه؟
🔍 نمادِ ∩ به چه معناست؟
این نماد به معنای اشتراک است.
فرض کنید مجموعهٔ A و مجموعهٔ B هر دو ۵ عضو دارند:
A = {1, 2, 3, 4, 5}
B = {3, 4, 5, 6, 7}
در این صورت، اشتراک A و B عبارت است از:
A∩B = {3, 4, 5}
اعداد ۳ و ۴ و ۵ در هر دو مجموعهٔ A و B مشترک هستند.
اما چرا در فرمول شمارهٔ یک، برای به دست آوردنِ احتمال A به شرط B، باید P(A∩B) را بر P(B) تقسیم کنیم؟
اجازه دهید توضیح دهم.
دوباره به نمودار یک نگاه کنید. همانطور که در این تصویر مشخص است، تمام اتفاقاتی که در دایرهٔ B ممکن است بیفتد، برای شما مهم نیست؛ بلکه اتفاق مشترک بین B و A برای شما مهم است (یعنی دیدن سلبریتی با توجه به دانشی که از محله خود دارید). پس باید احتمال مورد علاقهتان را تقسیم بر کلیه احتمالات ممکن بکنید. به همین دلیل p(A∩B) را بر p(B) تقسیم میکنیم.
بار دیگر به فرمول شمارهٔ یک نگاه کنید:
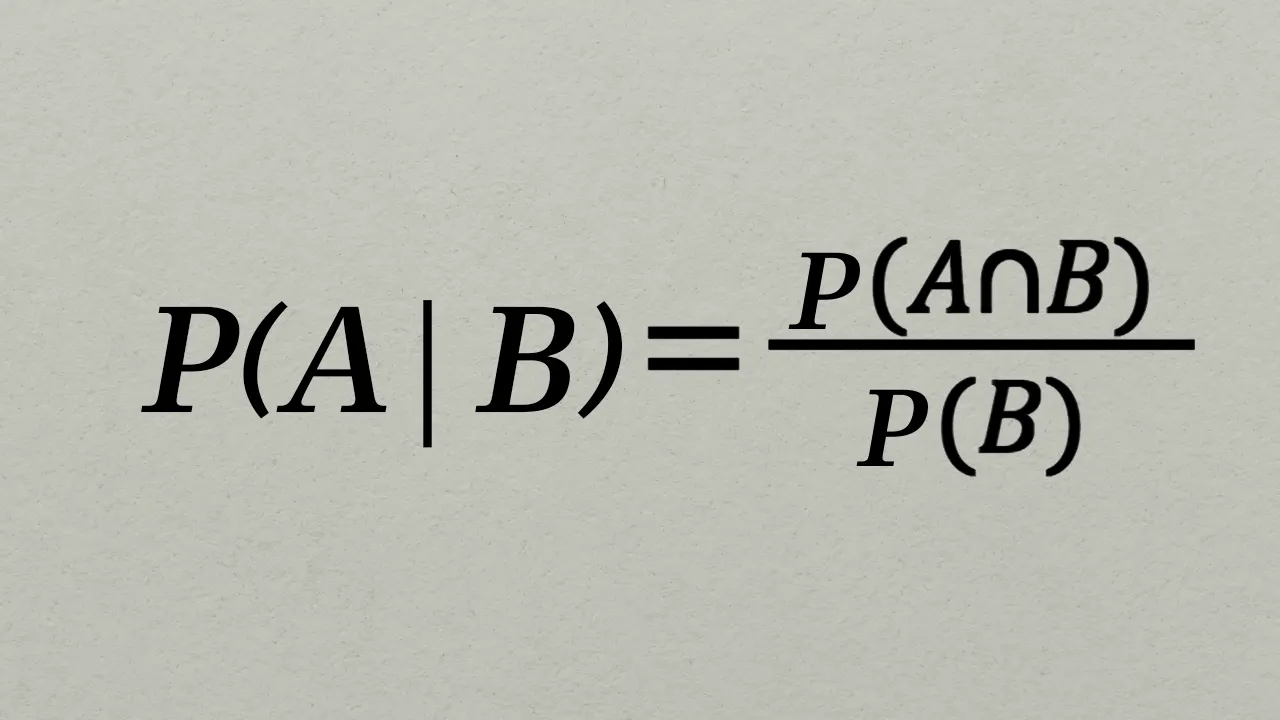
همین فرمول را میتوان به شکل زیر هم نوشت:
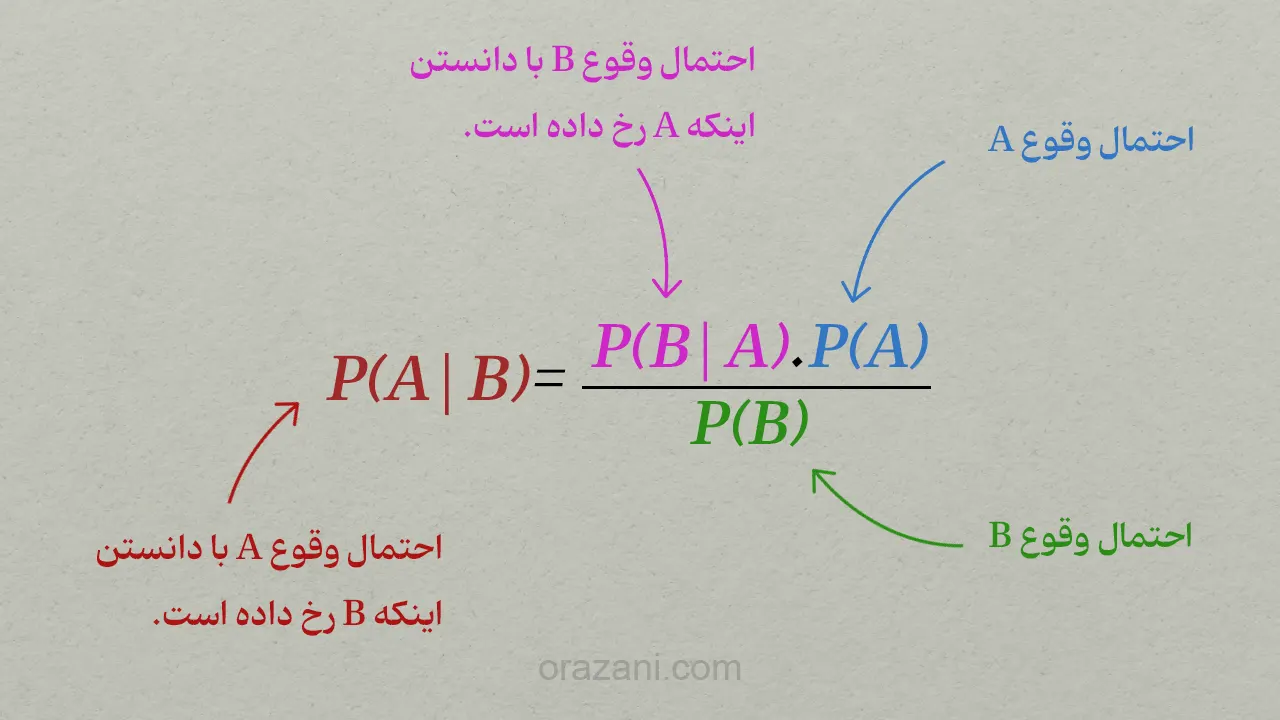
این فرمول «قضیهٔ بیز» نامیده میشود.
🔍 برای مطالعهٔ بیشتر: فرمول قضیهٔ بیز از کجا آمده است؟
چرا احتمال A به شرط B را میتوان به شکل فرمول بالا هم نوشت؟
برای پاسخ به این پرسش، از همان فرمول احتمال شرطی کمک میگیریم.
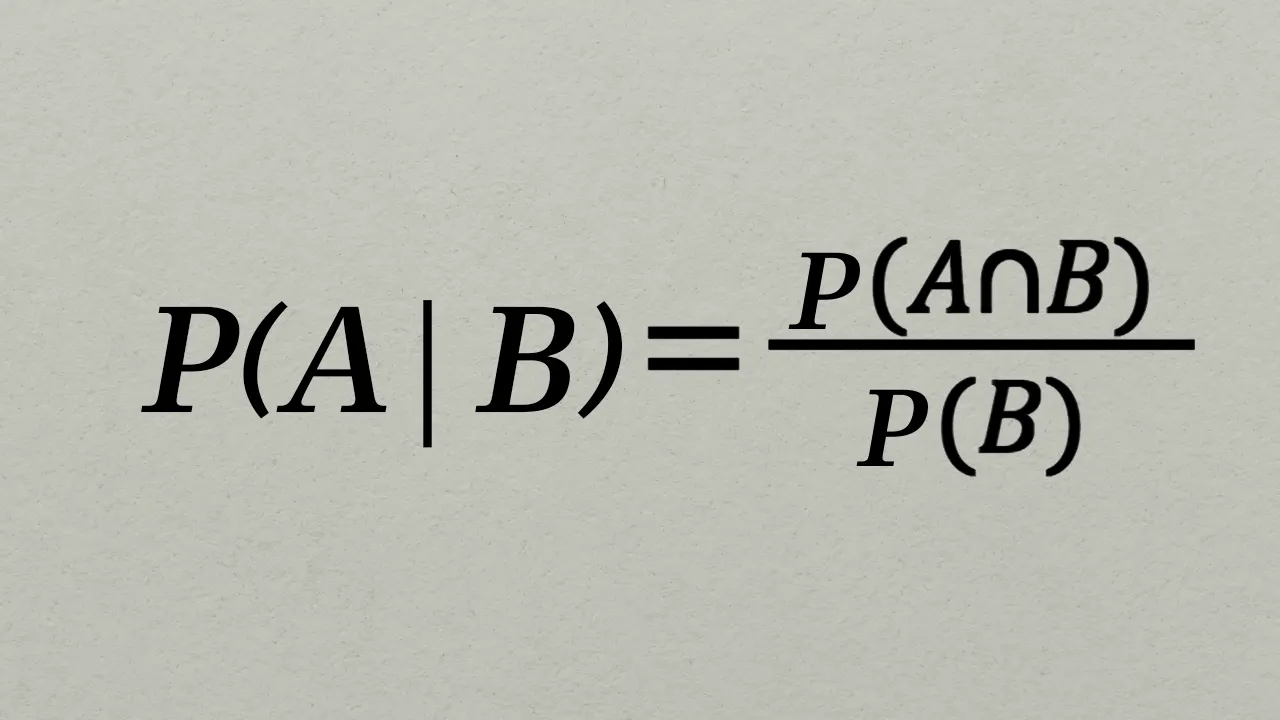
حال جای A و B را در این فرمول عوض میکنیم. یعنی به جای احتمال A به شرط B، این بار احتمال B به شرط A را محاسبه میکنیم. در این صورت داریم:
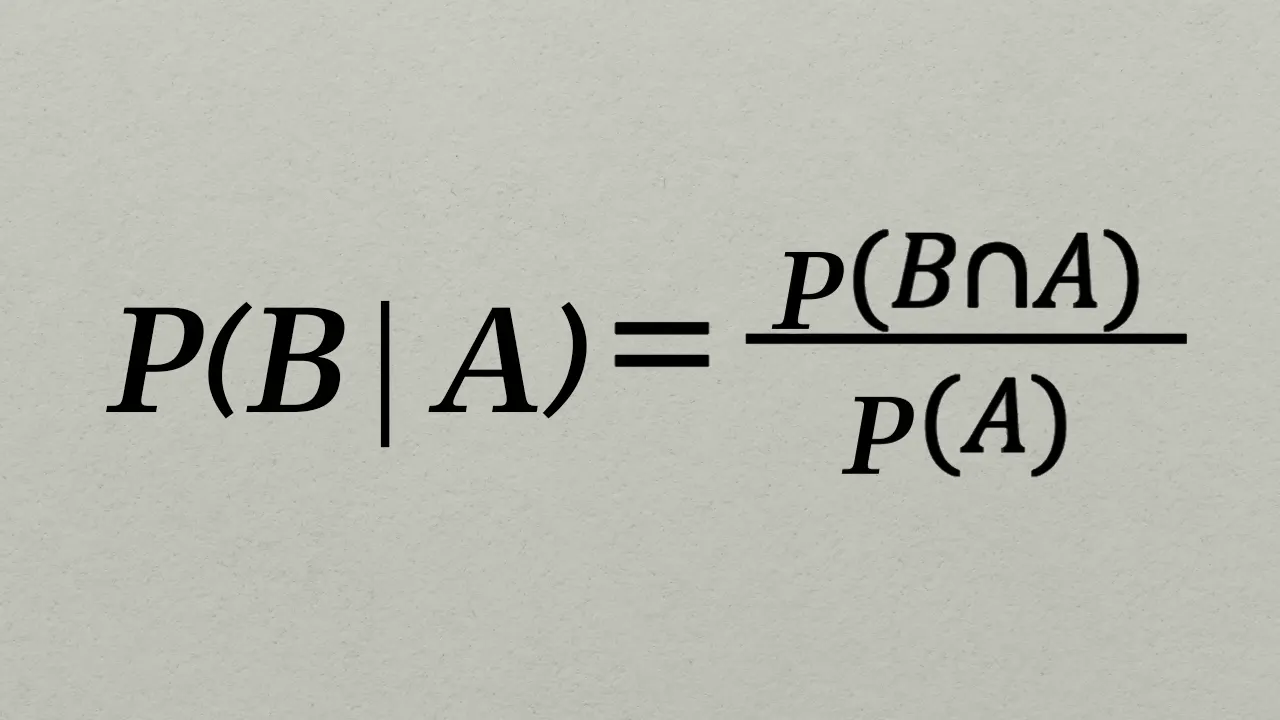
حالا از این فرمول، مقدار معادل P(A∩B) را استخراج میکنیم و در فرمول اول قرار میدهیم.

این هم از اثبات قضیهٔ بیز!
حالا با خیال راحت میتوانید از آن برای برآورد احتمال دیدن سلبریتی محبوبتان استفاده کنید.
میدانم این فرمولها ممکن است خستهتان کرده باشد. اشکال ندارد؛ به نظرم فعلاً این متن را به کناری نهید و به کار دیگری مشغول شوید. این تنها شما نیستید که در مواجهه با چنین متنهایی خسته میشوید. من هم باید چنین متنهایی را چند بار بخوانم تا به درستی آنها را بفهمم.
با هوشِ متوسطی که دارم، ناگزیر از تکرار هستم. بارها پیش آمده است که سر کلاس یا کارگاههای آمار، از مُدرس یک پرسش را چند بار پرسیدهام. :)
پس اگر باهوش هستید، قدرش را بدانید و اگر هم مثل من هوش متوسطی دارید، باید با تکرار و پرسش و کمک گرفتن از دوستانتان یاد بگیرید.
کجای این جستار برایتان نامفهوم بود؟ آمار بیز جالب نیست؟ درست است که تا حدی دشوار است اما مبحث جالبی است. ما دائماً در حال بهروز کردن احتمالات با تکیه بر دانشی هستیم که کسب میکنیم. اطلاعات دائماً بهروز میشوند و ما باید تا آنجا که میتوانیم اطلاعات جدید را در دایرهٔ اطلاعات قبلی وارد کنیم.
یادم رفت بپرسم، سلبریتی محبوب خود را از نزدیک دیدهاید؟ :)

دورهٔ عملیِ صفر تا صدِ آمار و روش تحقیق
موفقیت در هر حرفه نیاز به دانش و مهارتهایی دارد. آمار و روش تحقیق از جمله دانش و مهارتهایی است که تسلط بر آن، فرصتهای ویژهای در مسیر شغلی و تحصیلی پیش رویتان خواهد گذاشت.
دورهٔ عملی صفر تا صدِ آمار و روش تحقیق بر اساس نیازهای واقعی شما و تشخیص نقاط قوت و ضعف آموزشهای موجود، برای یادگیریِ گامبهگام، عملی و کاربردی طراحی شده است.
🎯 در طول این دوره، دانش و مهارت لازم برای انجام یک پروژهٔ پژوهشی، فهم بهتر مقالات روز و بهکارگیری آمار در مشاغل مختلف علوم اجتماعی، از جمله روانشناسی را کسب خواهید کرد.
💥 این دوره تنها به آموزشِ نظری محدود نمیشود. بخش زیادی از مطالب آمار و روش تحقیق از جنس مهارت است و نیاز به تمرین و تکرار دارد. در این دوره با کمک آزمونهای خود-ارزیابی، تکالیف و پروژههای عملی و کاربردی، شما را همراهی خواهیم کرد تا برای تجربههای واقعی در مسیر تحصیلی و شغلی خود آماده شوید.
🔥 امکانات و فرصتهای ویژهای در طراحی این دوره در نظر گرفته شده است که آن را در مقایسه با دورههای مشابه، تبدیل به دورهای خاص میکند!
هدف ما پیش از هر چیز، رفع موانع یادگیری و رشد جامعهٔ علمی است. :)
برای مشاهدهٔ نحوهٔ برگزاری دوره، امکانات، دستاوردها و سایر جزئیات، روی دکمهٔ زیر کلیک کنید.


نظرات، سؤالات و انتقادات خود را در بخش انتهای همین صفحه، به صورت کامنت مطرح کنید.

اگر این مطلب برایتان مفید بود، آن را با دیگران به اشتراک بگذارید و به رشد جامعهٔ علمی کمک کنید.
🔻 اگر این جُستار را دوست داشتید، احتمالاً جستارهای زیر نیز برایتان مفید خواهد بود:
🔗 روانشناسی و آمار: این دلبرِ دیو صفت!
🔗 فریبِ بازی با آمار را نخور: بازی با آمار و شهروندِ آگاه!
🔗 آیا روانشناسی «علم» است؟
